How To Find The Distance Between To Points
Distance Between 2 Points

Quick Explanation
When nosotros know the horizontal and vertical distances between two points nosotros can summate the straight line altitude like this:
altitude = √ a2 + b2

Imagine you know the location of two points (A and B) like here.
What is the distance between them?
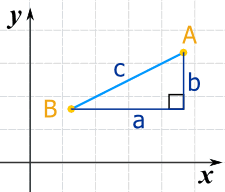
We can run lines down from A, and along from B, to make a Right Angled Triangle.
And with a niggling help from Pythagoras we know that:
a2 + btwo = c2
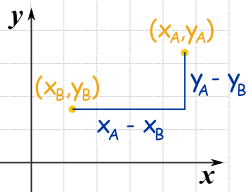
At present label the coordinates of points A and B.
xA means the x-coordinate of bespeak A
yA means the y-coordinate of signal A
The horizontal distance a is (xA − xB)
The vertical altitude b is (yA − yB)
At present nosotros tin solve for c (the altitude betwixt the points):
Start with: c2 = a2 + bii
Put in the calculations for a and b: c2 = (xA − 10B)two + (yA − yB)2
Foursquare root of both sides: c = √ (tenA − tenB)two + (yA − yB)ii
Examples
Example 1
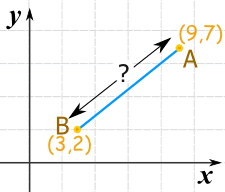
Fill up in the values: c = √ (9 − three)2 + (7 − 2)2
Summate: c = √ 6two + 52
c = √ 36 + 25
c = √ 61
c = 7.8102...
Example two
Information technology doesn't affair what order the points are in, because squaring removes any negatives:
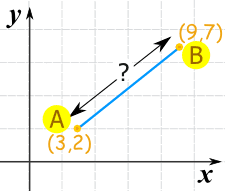
Fill in the values: c = √ (iii − nine)two + (two − 7)2
Calculate: c = √ (−half dozen)two + (−5)2
c = √ 36 + 25
c = √ 61
c = 7.8102...
Example 3
And here is some other example with some negative coordinates ... it all still works:
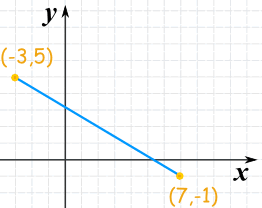
Make full in the values: c = √ (−3 − 7)2 + (5 − (−1))2
Summate: c = √ (−10)ii + half dozen2
c = √ 100 + 36
c = √ 136
c = 11.66...
(Note √136 can be further simplified to two√34 if y'all desire)
Try Information technology Yourself
Drag the points:
images/dist2pts.js
Three or More Dimensions
It works perfectly well in 3 (or more!) dimensions.
Square the difference for each axis, and so sum them up and have the square root:
Distance = √ (tenA − tenB)ii + (yA − yB)ii + (zA − zB)2

Example: the distance between the two points (8,ii,6) and (three,5,7) is:
= √ (viii−3)2 + (2−v)ii + (6−seven)2
= √ vtwo + (−3)2 + (−1)2
= √ 25 + 9 + i
= √ 35
Which is about 5.9
Read more at Pythagoras' Theorem in 3D
513, 514, 1148, 1149, 2994, 2995, 2996, 2997, 4034, 4035
Source: https://www.mathsisfun.com/algebra/distance-2-points.html
Posted by: santanafaccons.blogspot.com


0 Response to "How To Find The Distance Between To Points"
Post a Comment